How to Adjust Imprecise Building Footprint in Python

Building footprint is one of important data when working in an urban area or a project related to urban planning and management. There are many ways to generate building footprint such as manual digitizing from a aerial photo or high resolution satellite imagery. There is also a faster way to extract automatically building footprint from Satellite imagery or LiDAR data using a specific software. No matter which way it is, imprecise footprint can be found in a dataset that could upset or distrust the quality of the data. 

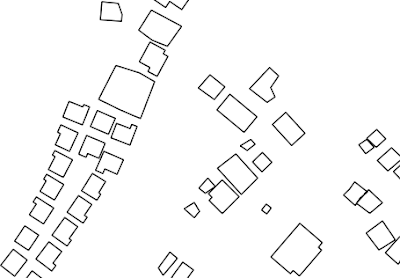
In this post I'll  share my experience when getting such a messy building footprint from manual digitizing as shown in figure 1. Throughout this post I will explain the algorithm how to adjust imprecise building footprint in particular rectangular building shape with perpendicular angle. Then I will also discuss how to implement the algorithm in Python, so you can get a full understanding from algorithm to the  implementation.

Figure 1. Imprecise Building Footprint

Building Footprint Adjustment Algorithm

Might be there are many approaches how to adjust imprecise building footprints. But in this post I will explain an approach based on my experience. The algorithm consist of several steps that applied geometry analytic calculation that we had studied in high school or university. So I think it's quite interesting to see how some calculations like calculating angle between two vectors, finding a line function, doing rotation matrix, etc, are applied in the algorithm. In figure 2 can be seen how the algorithm works.

Figure 2. Building Adjustment Process

Now let's break down the algorithm.

1. First step is finding a corner angle. The angle between two vectors can be calculated using dot product as in the following formula. \[a\cdot b=|a|\:|b|\:cos\:\theta\]

Figure 3. Vector Angle

2. If the corner angle is not 90 degrees, then one vector must be rotated. So the two vectors will be perpendicular to each other. The rotation can be done using rotation matrix as in the following formula where $\theta'=90^{\circ}-\theta$.

\[\begin{vmatrix} x'\\y' \end{vmatrix}=\begin{vmatrix}x\\y\end{vmatrix}\begin{vmatrix}cos\: \theta' & -sin\: \theta'\\sin\: \theta' & cos\: \theta'\end{vmatrix}\]     

3. Next step is to find the intersection point($x_i,y_i$) between the rotated vector and another adjacent vector. For that we need to find both those vector line functions. If the function for the rotated vector is $y_r=m_rx+b_r$ and the adjacent one is $y_c=m_cx+b_c$, then we can compute the intersection point as follow.

\[m_rx+b_x=m_cx+b_c\] \[m_rx-m_cx=b_c-b_r\]\[x(m_r-m_c)=b_c-b_r\]\[x=\frac{b_c-b_r}{m_r-m_c}\]

Here $x$ is equal to $x_i$, so after getting $x$, substitute it into one of line function to get $y_i$.

That's all three steps that are required in this algorithm. Those steps will be applied at each point in a building in order to get a precise rectangular building shape.

Let's implement the algorithm in Python.

Building Footprint Adjustment in Python

To do the adjustment using the algorithm that was already explained above, some functions have to be created such as: line function, vector length, vector angle, rotation matrix, point intersection and lastly a function to do the adjustment process.

The function below is the line function that returns the gradient(m) of a line and intercept b. The input for this function are coordinates of a line xy1 and xy2.

#lINE FUNCTION
def line(xy1,xy2):
    x1,y1=xy1[0],xy1[1]
    x2,y2=xy2[0],xy2[1]
    dx=x2-x1
    dx=0.1 if dx==0 else dx
    m=(y2-y1)/dx
    b=y1-m*x1
    return(m,b)

Two following functions are functions to calculate vector length and vector angle. The vector_length function is quite simple that takes a vector which represents in x and y. This function will be used in the vector_angle function to calculate the angle between two vectors using the dot product equation.

#VECTOR LENGTH FUNCTION
def vector_length(x,y):
    l=np.sqrt(x**2+y**2)
    return l

#VECTOR ANGLE FUNCTION
def vector_angle(xy0,xy1,xy2):
    vx1=(xy1[0]-xy0[0])
    vy1=(xy1[1]-xy0[1])
    vx2=(xy2[0]-xy0[0])
    vy2=(xy2[1]-xy0[1])
    theta=np.arccos((np.dot([vx1,vy1],[vx2,vy2]))/(vector_length(vx1,vy1)*vector_length(vx2,vy2)))
    theta_deg=(theta/np.pi)*180
    return theta_deg

After getting an angle at a corner of a building using the vector_angle function, a respective vector will be rotated to be perpendicular to each other. For this a rotation function which is called rot_xy is created. The input for this function is rotation angle $\theta$ and a coordinate of adjacent vector.

#ROTATION FUNCTION
def rot_xy(theta,xy):
    xr=xy[0]*np.cos(theta)-xy[1]*np.sin(theta)
    yr=xy[0]*np.sin(theta)+xy[1]*np.cos(theta)
    return np.array((xr,yr))

Next step is to find an intersection point between the rotated line with the next adjacent line. This can be done with the following xy_intersect function.

#POINT INTERSECTION FUNCTION
def xy_intersect(xy1,xyu,xy2,xy3):
    m1,b1=line(xy1,xyu)
    m2,b2=line(xy2,xy3)
    x_inter=(b2-b1)/(m1-m2)
    y_inter=m2*x_inter+b2
    return np.array((x_inter,y_inter))

Lastly a function that combines all the steps for footprint adjustment is created. I called this function adjust_point. This function takes a list with four variables: there are center or mid point (mp) where the angle will be adjusted, back point (bp), forward point (fp) and  front forward point (ffp).  

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25

#ADJUSTMENT FUNCTION def adjust_point(b): bp,mp,fp,ffp=b[0],b[1],b[2],b[3] #find vector angle theta=vector_angle(mp,bp,fp) if round(theta,0)!=90.: theta_rd=90.-theta xyr=rot_xy(np.radians(theta_rd),fp-mp) #find intersect coordinate xc,yc=xy_intersect(mp,xyr+mp,fp,ffp) #check angle at current point check_theta=vector_angle(mp,bp,xyr+mp) #check if angle prependicular if round(check_theta,0)!=90.: xyr=rot_xy(np.radians(-theta_rd),fp-mp) xc,yc=xy_intersect(mp,xyr+mp,fp,ffp) update_theta=vector_angle(mp,bp,(xc,yc)) else: xc,yc=fp[0],fp[1] return np.array((xc,yc))

So far all the required functions have been created. Save it into a python file which is called building_adjustment_function.py.

Now, let's take some buildings coordinates. In the code below, I defined five buildings ba, bb, bc, bd and be. All the coordinates are stored in tuples within a list.

 

import matplotlib.pyplot as plt
import numpy as np

from building_adjustment_function import *
 

#BUILDING COORDINATES
ba=[(5.,10.),(6.,15.),(10.,16.),(9.,10.)]
bb=[(15.,5.),(14.,10.),(20.,11.),(21.,8.),(25.,9.),(25.,4.)]
bc=[(5.,16.),(1.,20.),(10.,25.),(12.,22.),(11.,20.),(15.,19.)]
bd=[(15.,15.),(17.,20.),(22.,21.),(20.,18.),(25.,18.),(22.,15.)]
be=[(5.,5.),(6.,8.),(11.,8.),(11.,11.),(14.,11.),(13.,5.)]
buildings=[ba,bb,bc,bd,be]

#PLOTTING PRE-ADJUSTED BUILDING
for b in buildings:
    x=[]
    y=[]  
    for i in b:
        x.append(i[0])
        y.append(i[1])
    x.append(b[0][0])
    y.append(b[0][1])
    plt.plot(x,y,'--',color='grey')
plt.show()

Next, each coordinate is stored in x and y list for plotting purpose using matplotlib library. In the figure 4 can be seen the buildings are plotted in dashed lines.

Figure 4. Pre-Adjustment Buildings

Now let's do the adjustment for the buildings. Firstly convert all coordinates into float, in case there is a coordinate not in float type. The following code will do the conversion. The converted coordinate is stored in the b_float list.

#CONVERT TO FLOAT
b_float=[]
for k in buildings:
    k=np.array(k).astype(float)
    b_float.append(k)

The code below is the code to do the adjustment. There are two loops in the code. The first one is a loop for each building, and the second one is for each point in a building. In the second loop, each point will be adjusted, and the adjusted point will be restored in the b_float list. Thus, the b_float list is the final result which contains all adjusted points.  

# RUNNING THE ADJUSMENT PROCESS    
for b1 in b_float:
    n_po=len(b1)
    for i in range(n_po):
        #condition for last two point
        if i==n_po-1:
            sb=[b1[i-1],b1[i],b1[0],b1[1]]
        elif i==n_po-2:
            sb=[b1[i-1],b1[i],b1[i+1],b1[0]]
        else:
            sb=[b1[i-1],b1[i],b1[i+1],b1[i+2]]
            
        #do the adjustment process
        xya=adjust_point(sb)
        try:
            b1[i+1]=xya
        except:
            pass

To see the result, let's plot the adjusted points, using the following code. 

#PLOTTING POST-ADJUSTMENT BUILDINGS
for b1 in b_float:
    x=[]
    y=[]  
    for i in b1:
        x.append(i[0])
        y.append(i[1])
    x.append(b1[0][0])
    y.append(b1[0][1])
    plt.plot(x,y,'ro')
    plt.plot(x,y,'k')

plt.axis('equal')
plt.show()

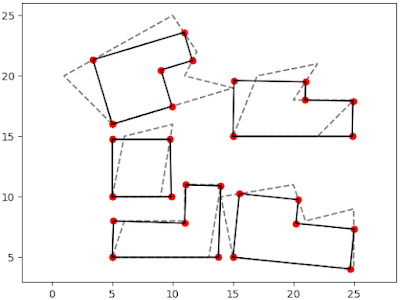
The adjusted building can be seen in the figure 5. In the figure can be compared the pre-adjustment buildings in dashed lines and post-adjustment buildings in black solid lines. 

Figure 5. Post-adjustment Building

Well done. The buildings now look more realistic in rectangular shape than before. I tested this algorithm and it works fine for buildings with angle not close to a straight line. If you want to try it by yourself, copy the codes into a Python file. If everything is fine, you should get the output as in figure 5. Anyway, I provide the code based on request. Make your request here if you want to get it.

That's all this tutorial about how to do adjustment for imprecise building footprint with Python. In this post we learnt about algorithm how to do the adjustment using some vector geometry calculations like vector angle, vector length, point intersection, etc. Overall the proposed algorithm and Python code might not cope all building shape with its complexity. But I hope you can get something from this post, and there is always room for improvement. Thanks for reading and happy coding! 

 Building Adjustment Geoanalytics Python